算法设计与分析期末复习

考试重点
1
2
3
4
5
6
7
第2章：1)理解基本概念：如算法输入规模的度量、运行时间的度量、算法效率函数的增长次数大小比较、
算法最优、最差和平均效率、算法效率表示的3 种符号的含义；2)掌握非递归和递归算法的效率分析方法(P370 附录 B反向替代法)；3)布置过的作业
第4章：1）领会减治法的基本思想 2)理解减常量和减常量因子的区别井会简单应用(如求a^n
第5章1)应用分治策略的大整数乘法：2)应用分治策略求二叉树相关问题(高度、层数、叶子等)
第6章1)领会变治法的基本思想：2)计算n次多项式的Horner[雷纳)法则： 3)计算a”的两种方法(从左到右，从右到左)：二进制幂：4）布置过的作业：
第8章: 1)背包问题(重点理解递归式的分析过程,并能灵活应用) 2) Warshall算法、Floyd算法3)布置过的作业
第9章:1)领会食心算法的设计思想并能简单应用。
分区算法
  1. 选择一个基准元素。这里我们选择数组的第一个元素作为基准，即 4。
  2. 初始化两个指针：一个指向数组的第一个元素（i = 0），另一个指向数组的最后一个元素（j = 8）。
  3. 从右向左移动指针 j，直到找到一个元素小于基准（4）。在这个例子中，j 指向的元素是 2，它小于 4。
  4. 从左向右移动指针 i，直到找到一个元素大于基准（4）。在这个例子中，i 指向的元素是 10，它大于 4。
  5. 交换 i 和 j 指向的元素。数组变为：[4, 1, 2, 8, 7, 12, 9, 10, 15]。
  6. 重复步骤 3 和 4，直到 i 和 j 相遇。在这个例子中，i 和 j 相遇在元素 8 的位置。
  7. 将基准元素（4）与 i 和 j 相遇位置的元素交换。数组变为：[2, 1, 4, 8, 7, 12, 9, 10, 15]。

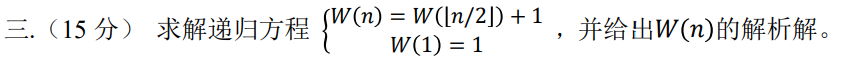
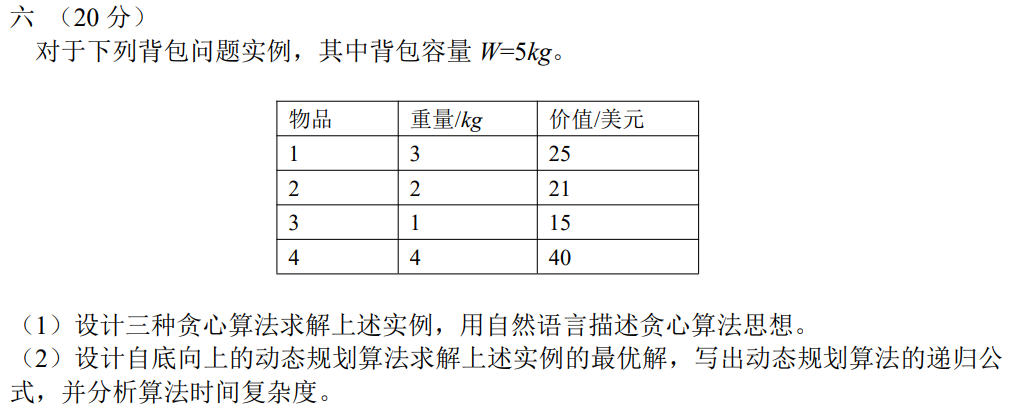
这道题目是一个典型的背包问题，需要求解如何在给定容量的背包中装入物品以使总价值最大化。下面详细讲解这道题的解法。

(1) 设计三种贪心算法

贪心算法并不一定能找到全局最优解，但它们在某些特定条件下能够提供近似解。这里我们设计三种不同的贪心算法：

贪心算法一：按单位重量价值排序

  1. 计算每个物品的单位重量价值（价值/重量）。
  2. 按单位重量价值从高到低排序。
  3. 从单位重量价值最高的物品开始，依次装入背包，直到背包容量满为止。

贪心算法二：按价值排序

  1. 按物品的总价值从高到低排序。
  2. 从价值最高的物品开始，依次装入背包，直到背包容量满为止。

贪心算法三：按重量排序

  1. 按物品的重量从低到高排序。
  2. 从重量最低的物品开始，依次装入背包，直到背包容量满为止。

(2) 底向上的动态规划算法

背包问题的动态规划解法可以找出全局最优解。我们使用一个二维数组 dp[i][w] 表示前 i 个物品在背包容量为 w 时的最大价值。

动态规划步骤：

  1. 初始化：dp[0][w] = 0 表示当没有物品可选时，最大价值为 0。
  2. 递推关系：
    • 如果不选第 i 个物品，dp[i][w] = dp[i-1][w]。
    • 如果选第 i 个物品，dp[i][w] = dp[i-1][w-weight[i-1]] + value[i-1]，前提是 w >= weight[i-1]。
  3. 状态转移：dp[i][w] = max(dp[i-1][w], dp[i-1][w-weight[i-1]] + value[i-1])。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public class Knapsack {
    public static int knapsack(int W, int[] weights, int[] values) {
        int n = weights.length;
        int[][] dp = new int[n + 1][W + 1];

        for (int i = 1; i <= n; i++) {
            for (int w = 0; w <= W; w++) {
                if (weights[i - 1] <= w) {
                    dp[i][w] = Math.max(dp[i - 1][w], dp[i - 1][w - weights[i - 1]] + values[i - 1]);
                } else {
                    dp[i][w] = dp[i - 1][w];
                }
            }
        }

        return dp[n][W];
    }

    public static void main(String[] args) {
        int W = 5;
        int[] weights = {3, 2, 1, 4};
        int[] values = {25, 21, 15, 40};
        System.out.println("Maximum value: " + knapsack(W, weights, values));
    }
}

时间复杂度分析：

  • 贪心算法：每个贪心算法的时间复杂度主要在排序阶段，时间复杂度为 O(nlog⁡n)O(n \log n)O(nlogn)。
  • 动态规划算法：时间复杂度为 O(nW)O(nW)O(nW)，其中 nnn 是物品数量，WWW 是背包容量。

总结：

  • 贪心算法易于实现，时间复杂度较低，但不保证最优解。
  • 动态规划算法时间复杂度较高，但能够保证找到全局最优解，适用于解决背包问题中的最优解问题。