【人工智能】期末复习
考前复习
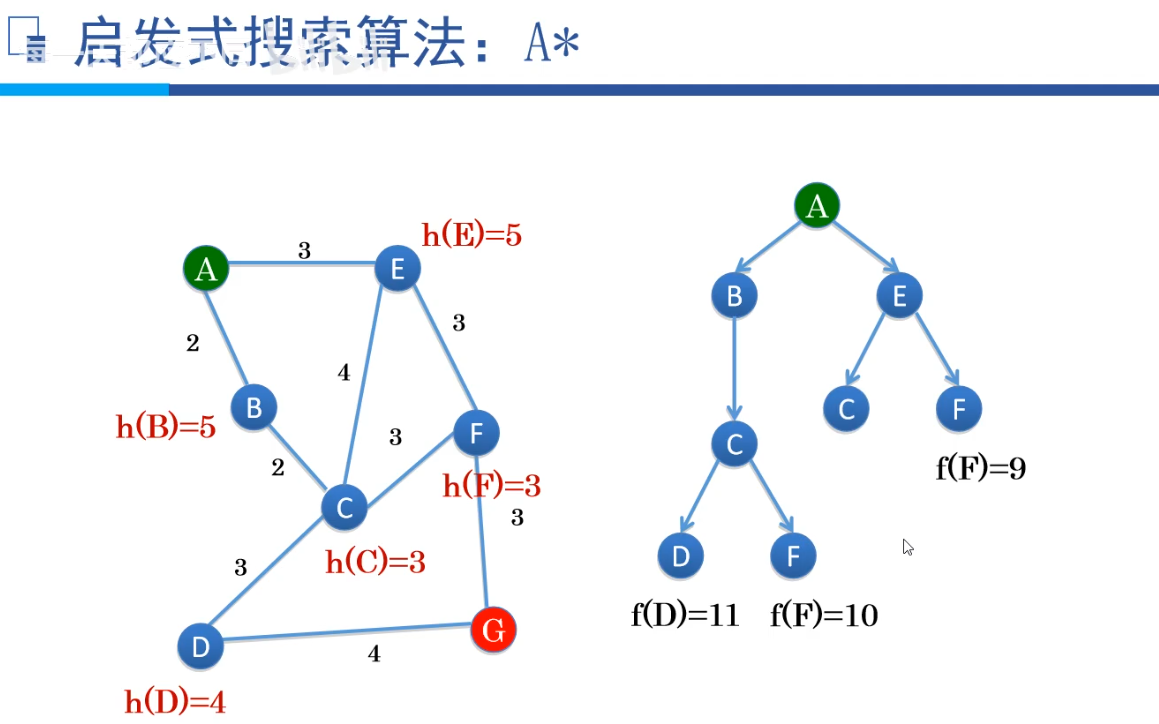
A算法中, f(n) = g(n) + h(n) g表示初始节点到x节点的距离,h表示x节点到目标节点的距离。f表示通过节点x的代价估计值,该值越小越好。 特点:效率高,无回溯。
举例说明:八数码问题:评价函数: h(n) = d(n) + W(n)
d(n)是搜索树中节点n的深度
W(n)用来计算节点n中位置错误数字的个数
同一层只选择估值最小的进行拓展。
A*是A的拓展算法,
f(n) = g(n) + h(n) 且 h(n) <= h*(n)
g(n)、 h(n)
定义同A算法;
h*(n):从N到目标节点的最短路径,采用ht (x)的下界h(x)为启发函数的A算法,称为A*算法。
特点特征:只要最短路径存在,就一定能够找到。
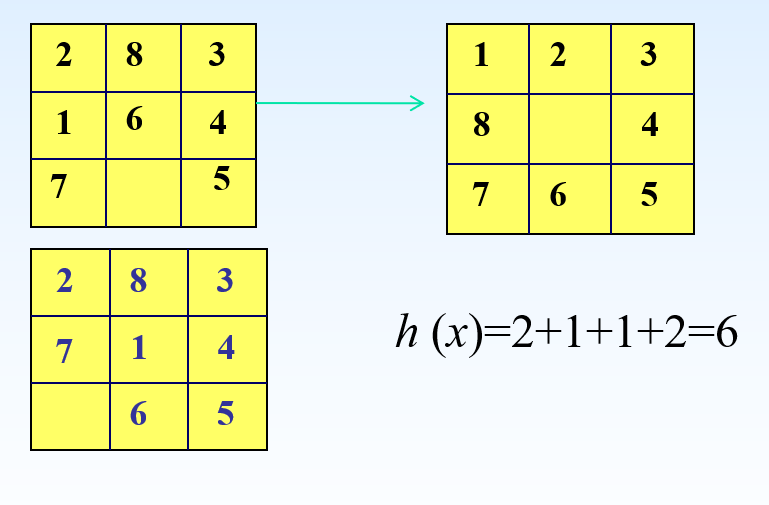
图中的公式 h(x)=2+1+1+2=6h(x) = 2 + 1 + 1 + 2 = 6h(x)=2+1+1+2=6 是通过计算每个棋子与其目标位置之间的曼哈顿距离得到的。曼哈顿距离是指棋子移动到目标位置需要走的水平和垂直步数之和。
以下是每个棋子从当前状态移动到目标状态的曼哈顿距离的计算过程:
- 棋子2:从(1,1) 移动到 (1,2) ,距离为 1 + 0 = 1
- 棋子8:从(1,2) 移动到 (2,1) ,距离为 1 + 1 = 2
- 棋子3:从(1,3) 移动到 (1,3) ,距离为 0 + 0 = 0
- 棋子1:从(2,1) 移动到 (1,1) ,距离为 1 + 0 = 1
- 棋子6:从(2,2) 移动到 (2,2) ,距离为 0 + 0 = 0
- 棋子4:从(2,3) 移动到 (2,3) ,距离为 0 + 0 = 0
- 棋子7:从(3,1) 移动到 (3,1) ,距离为 0 + 0 = 0
- 棋子5:从(3,3) 移动到 (3,2) ,距离为 0 + 1 = 1
总结起来,所有棋子的曼哈顿距离之和为: h(x)=1+2+0+1+0+0+0+1=5h(x) = 1 + 2 + 0 + 1 + 0 + 0 + 0 + 1 = 5h(x)=1+2+0+1+0+0+0+1=5
请注意,我发现公式 h(x)=2+1+1+2=6h(x) = 2 + 1 + 1 + 2 = 6h(x)=2+1+1+2=6 中似乎有误。上面的计算应该是准确的曼哈顿距离总和。根据我刚才的计算结果,正确的曼哈顿距离之和应该是 5。








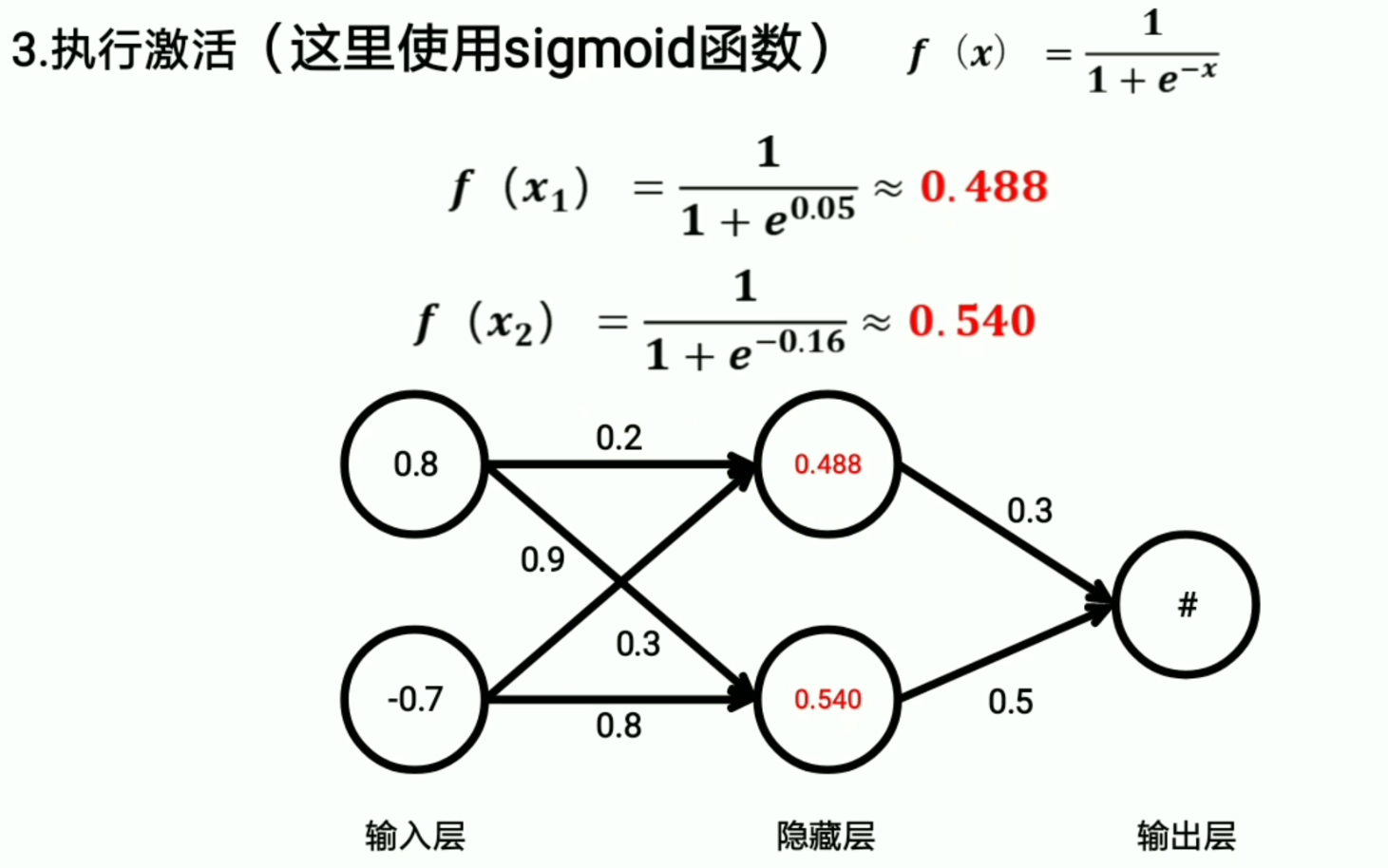
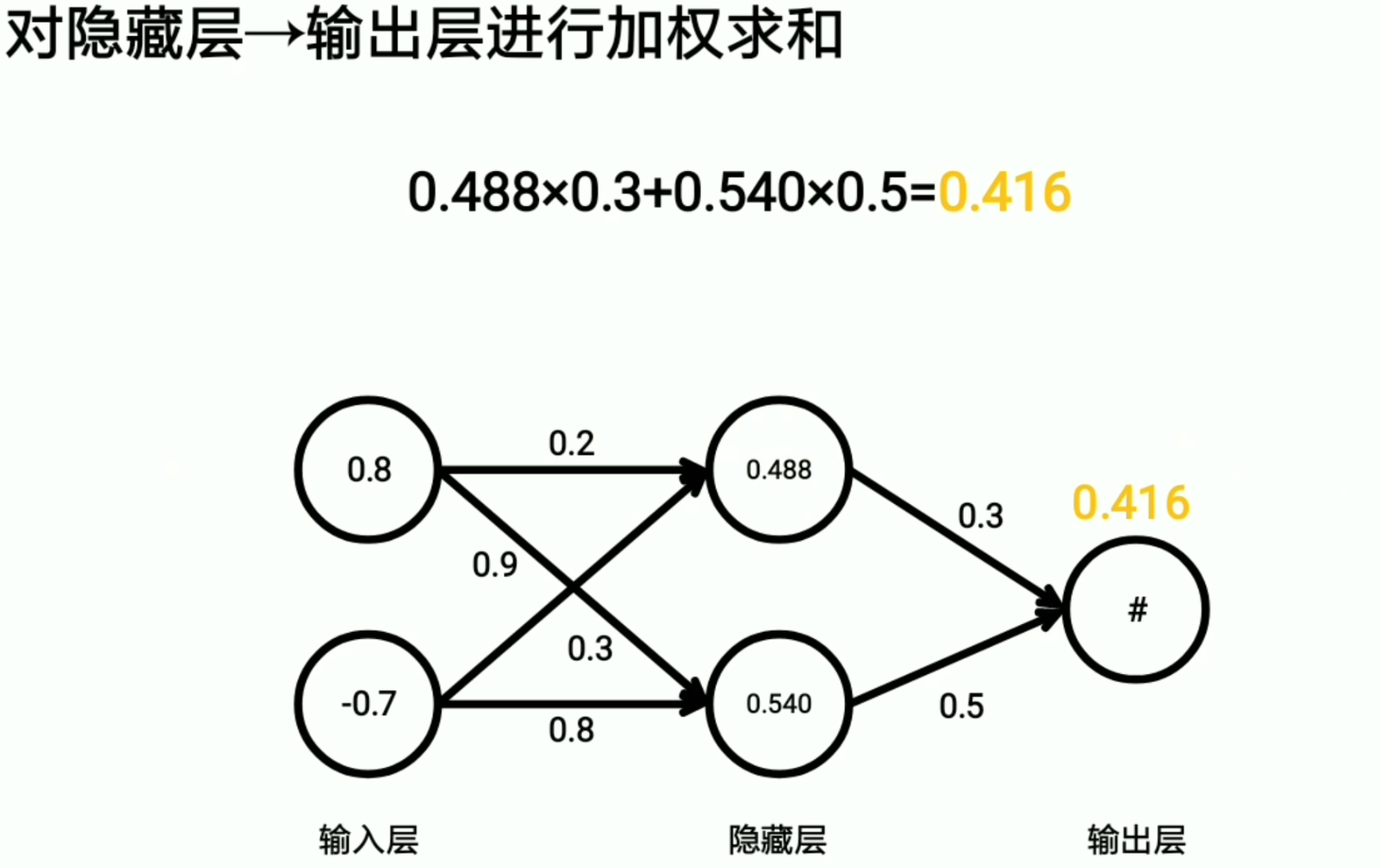
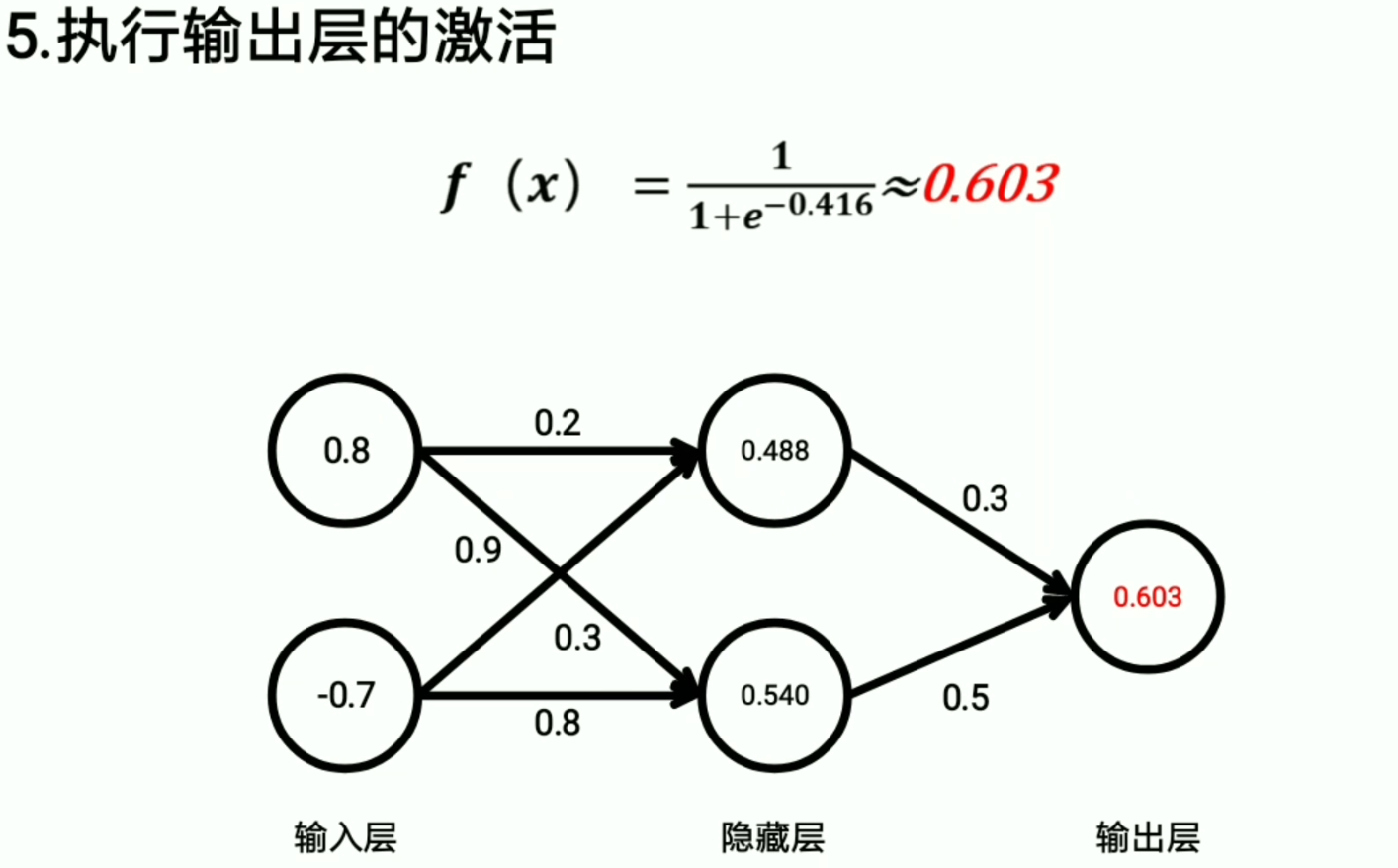
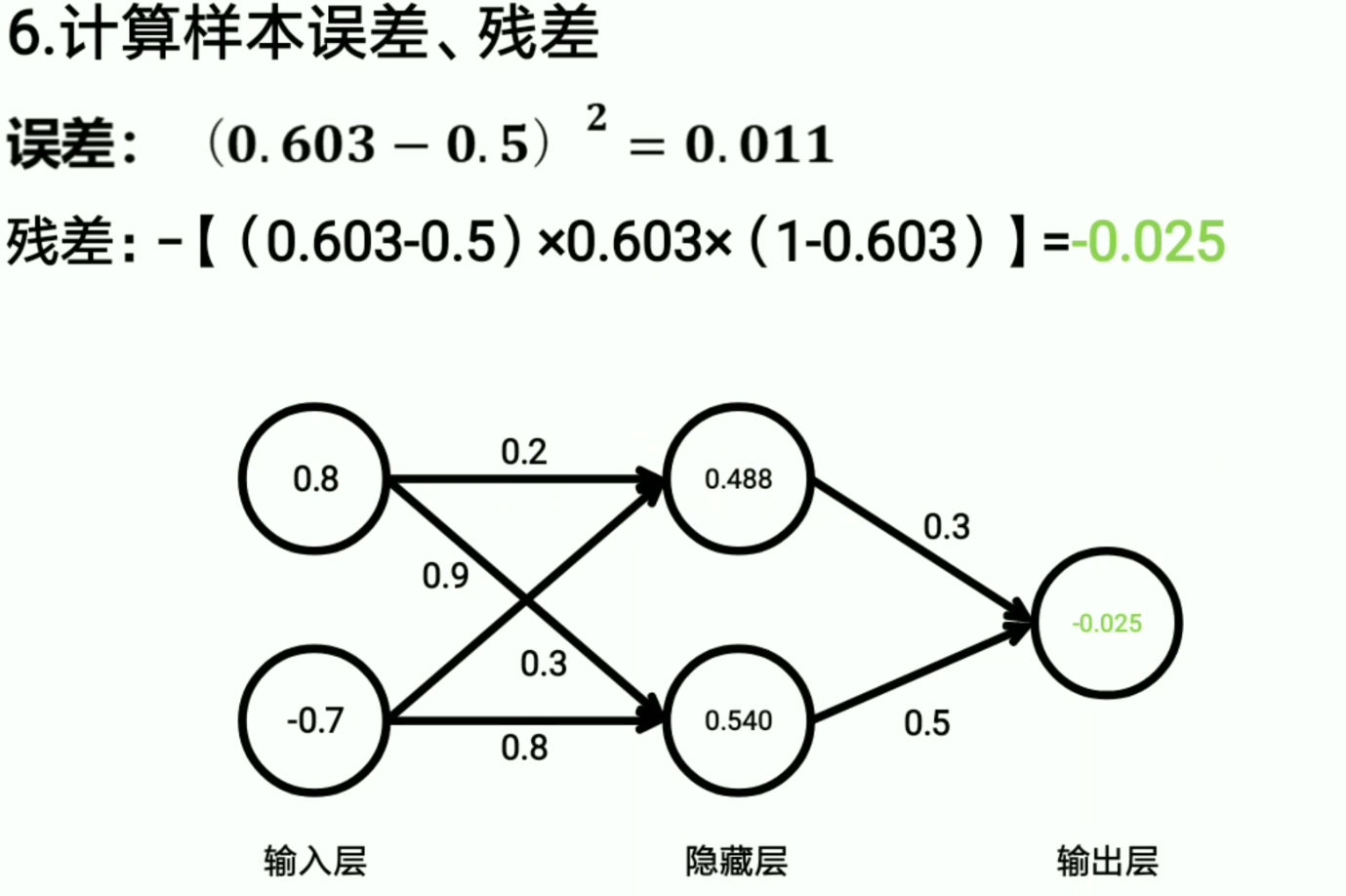
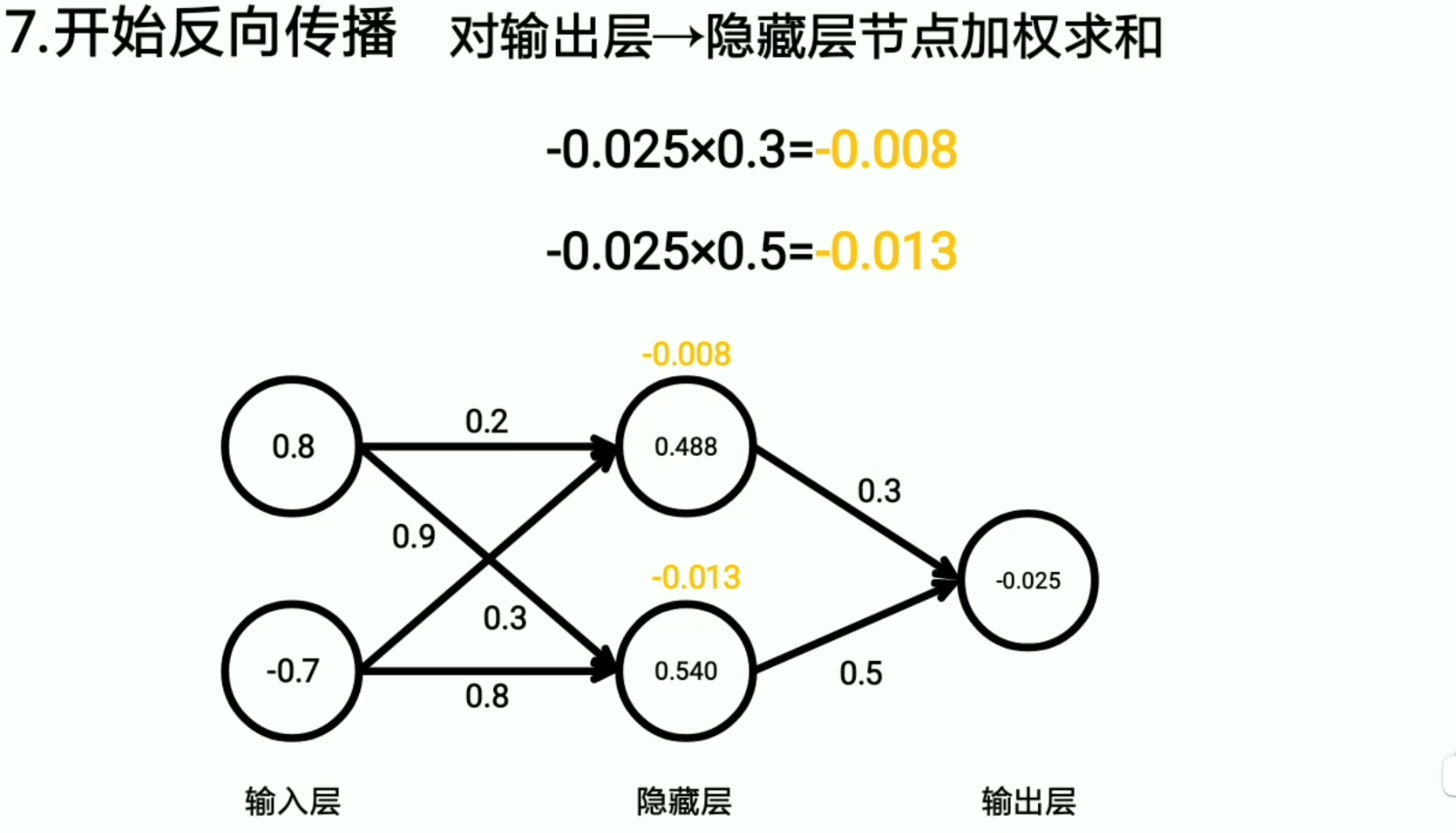
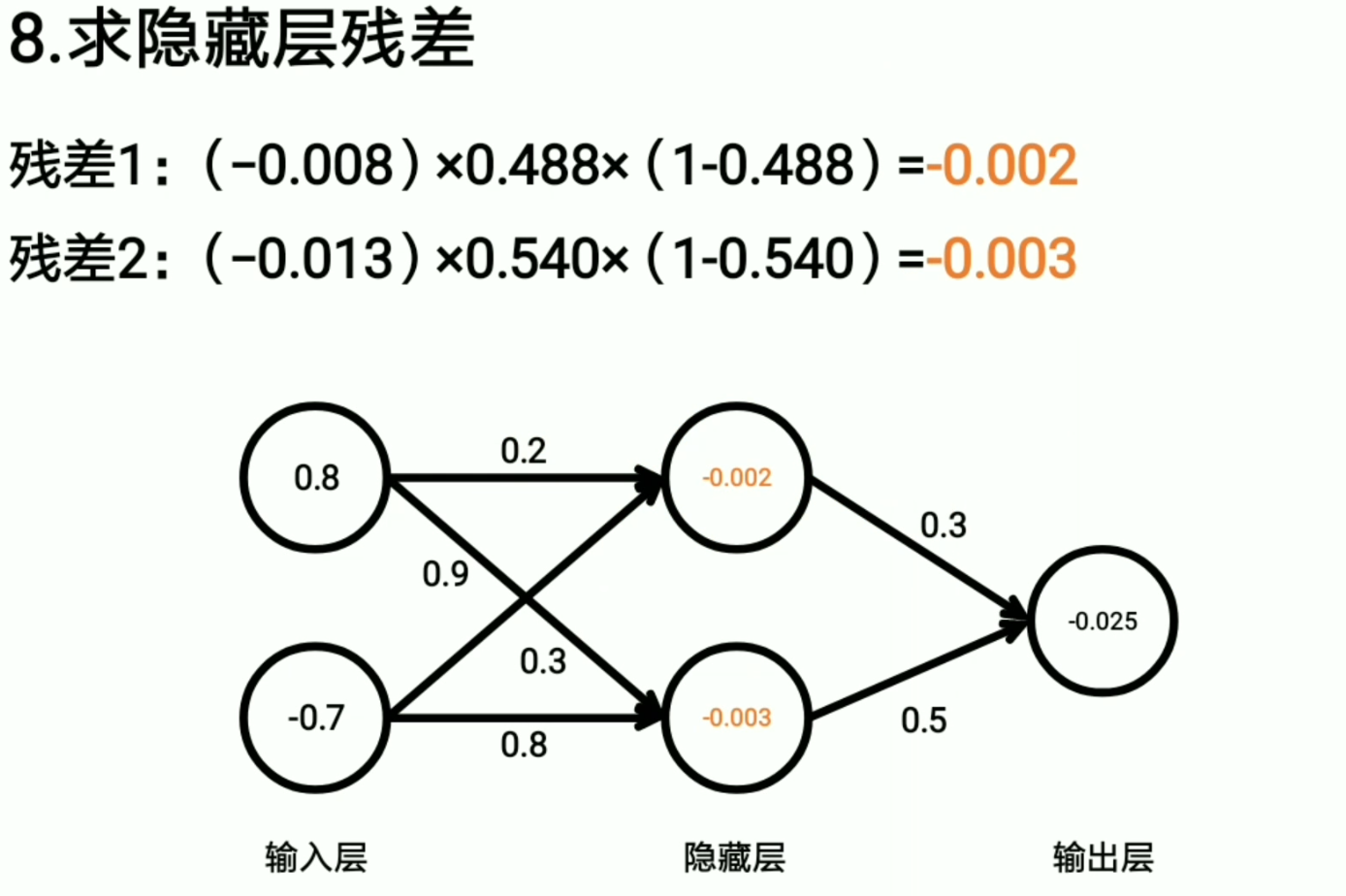
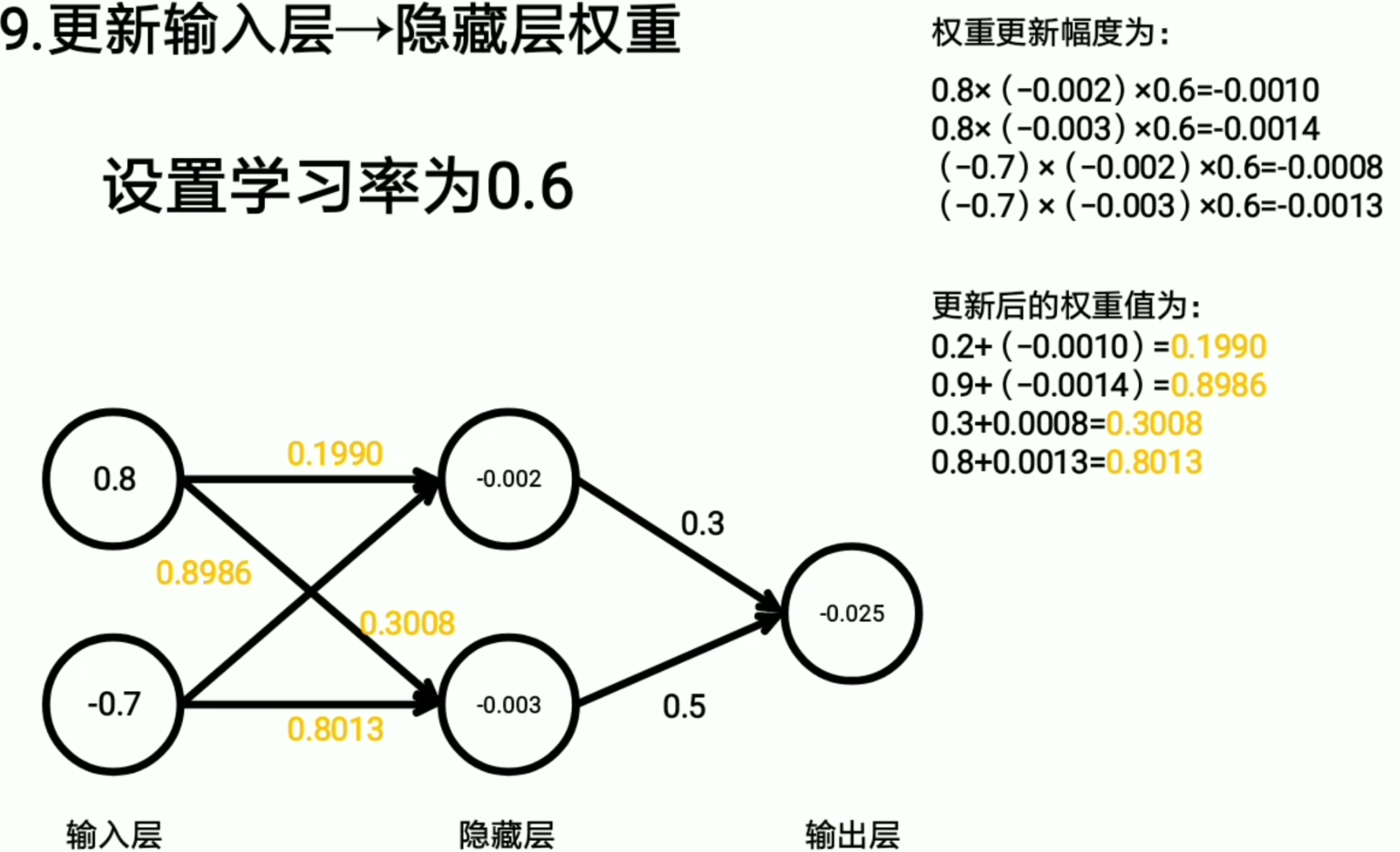
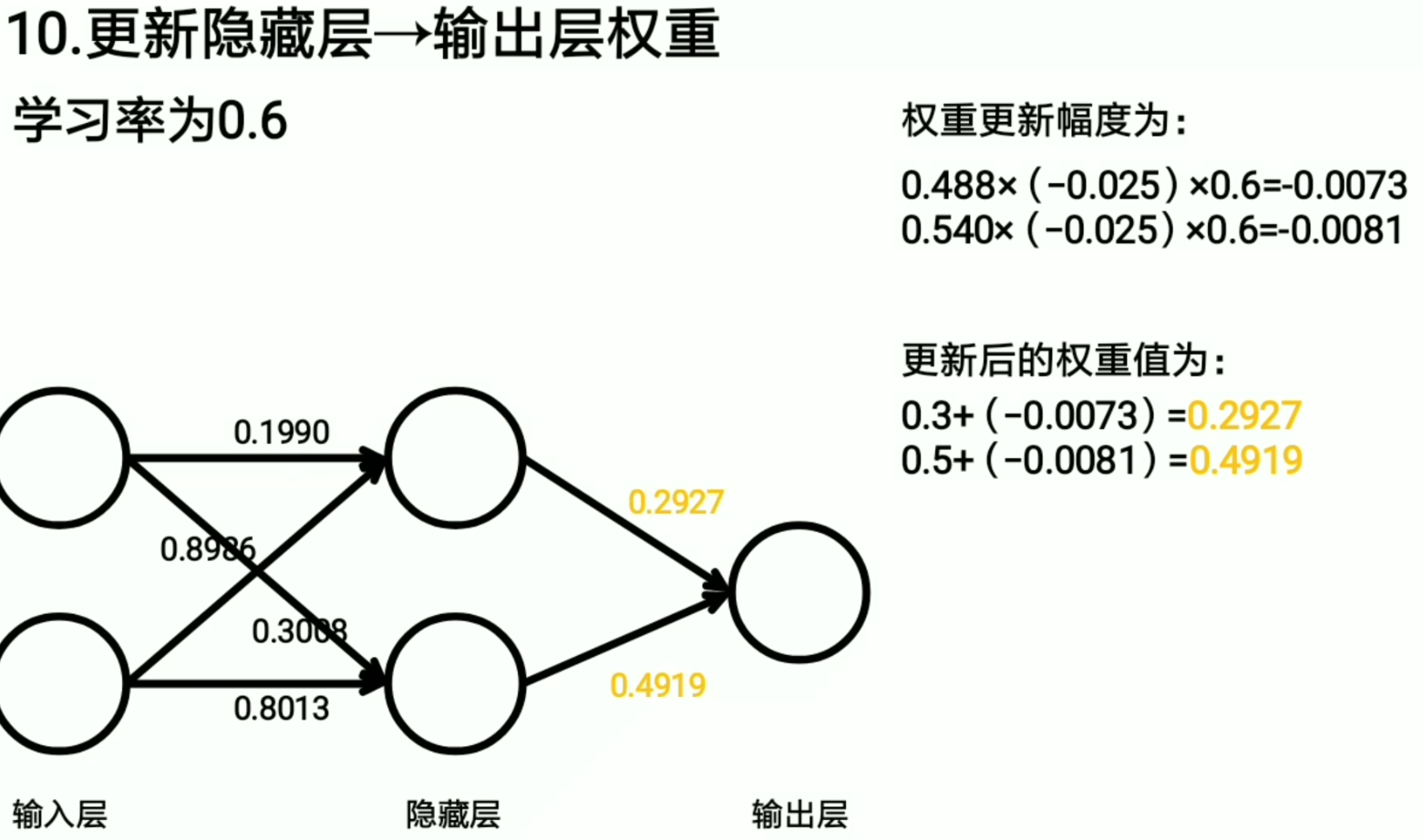


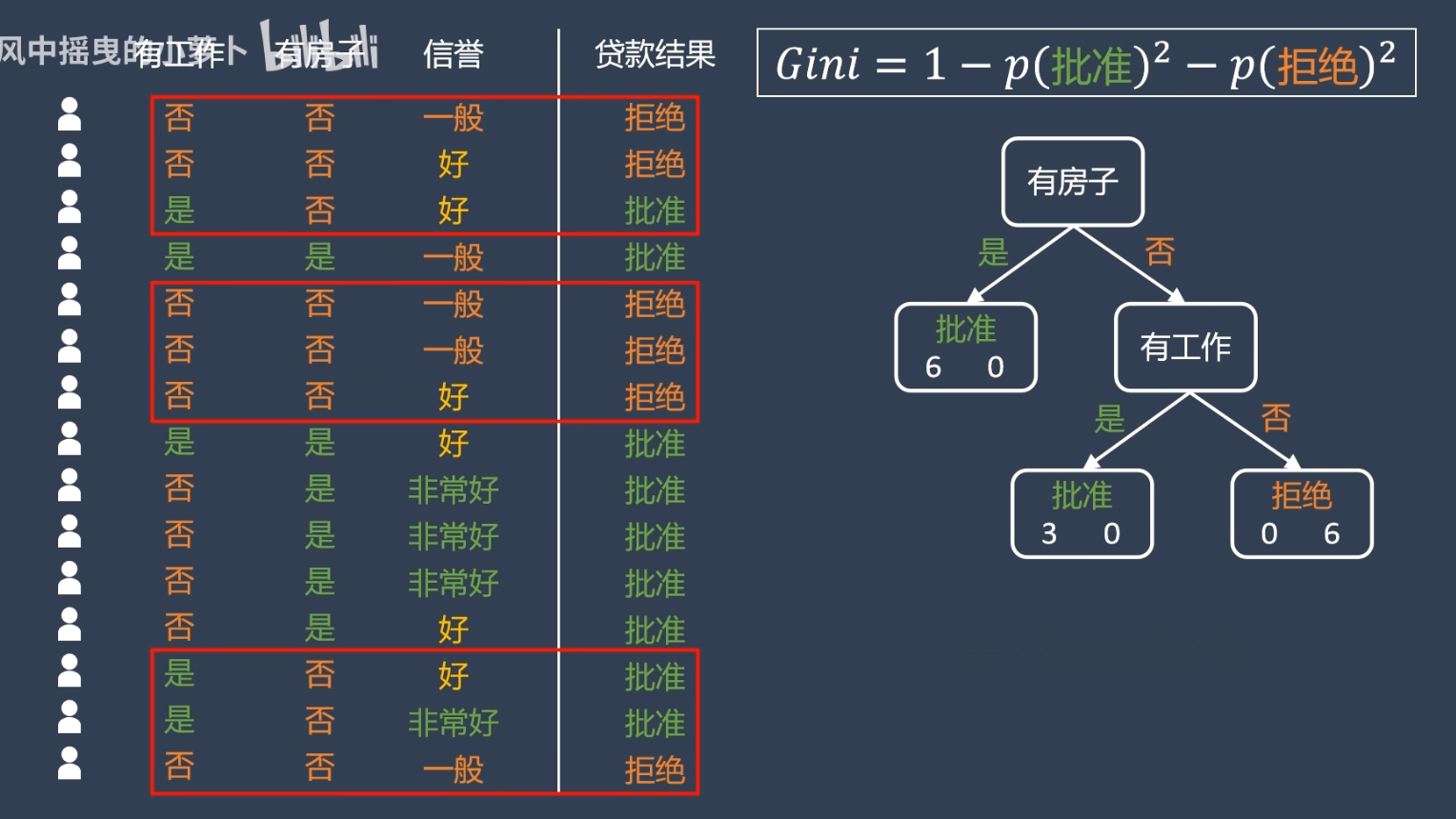
所以我们只需要选择基尼系数最小的来作为决策树的标准就行




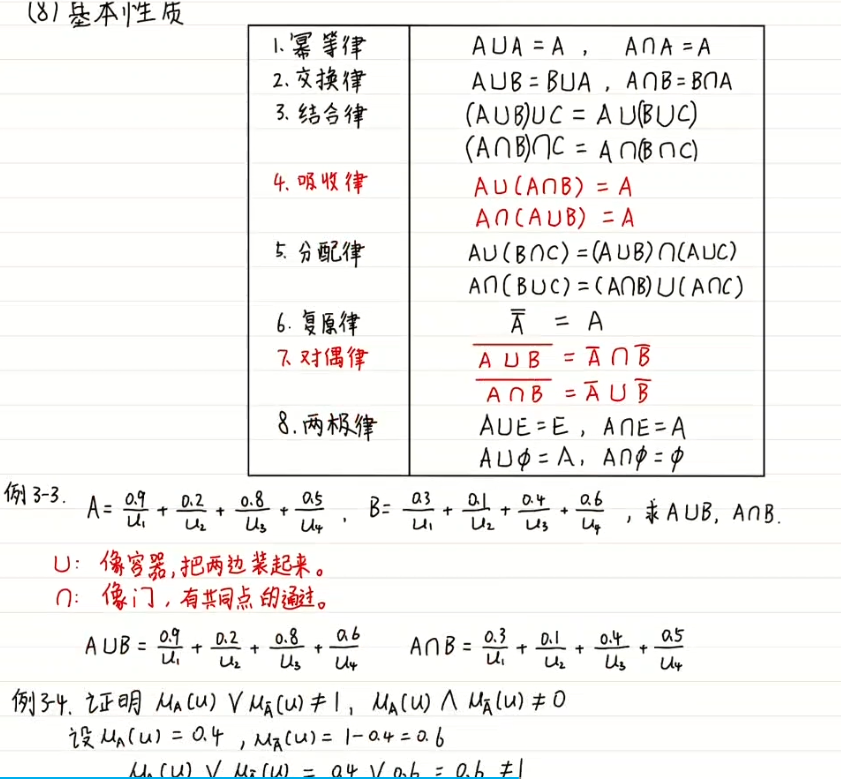
1推理
根据已知的一些命题,按照一定的法则,去推
断一个新的命题的思维过程和思维方式。即从已知
条件求未知结果的思维过程,就是推理。
2模糊推理
模糊逻辑推理是不确定性推理方法
之一,其基础是模糊逻辑。
它是一种以模糊判断为前提,运行
模糊语言规则,推理出一个新的、近似
的模糊判断结论的方法。


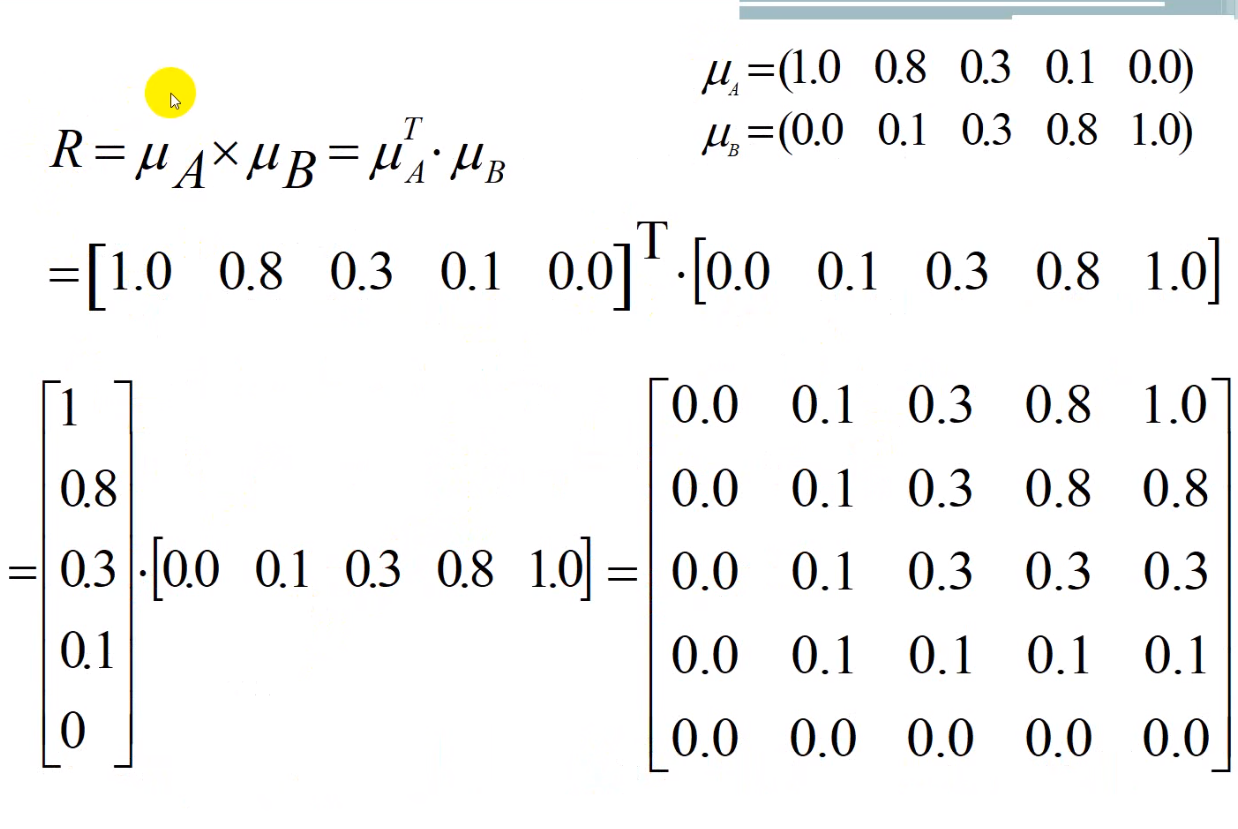


考后总结
开卷考试了,虽然题目感觉挺抽象的,但是过了。压线通过。我觉得过和不过,就是在于复习到没到位,像这个考试,课本真的太多内容了,看不过来的。老师通常也不会勤快出卷子,就可以直接找往年卷子来看,做一遍背一遍,直到看着题目就能把答案快速写下来就算复习到位了。