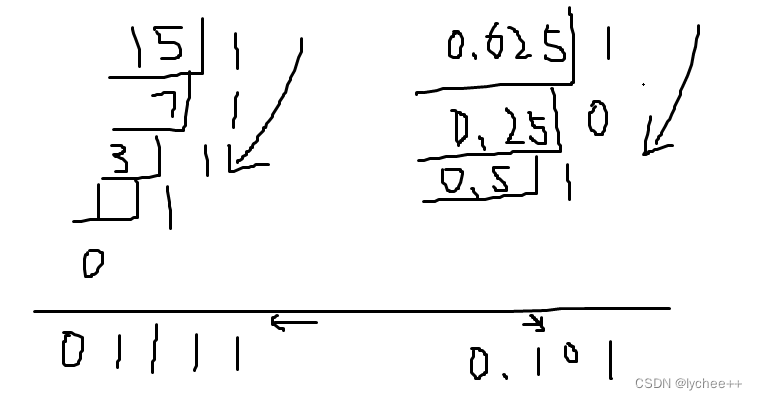# 【蓝桥杯备赛】:1.位运算
前言:请遵循 ==问题->思路->实践->题解==的方式学习
位运算的重要性质
& (与)
与的有趣性质
- 判断奇数还是偶数
任何数只要和1(0x00000001)进行&,如果等于1则是奇数,如果等于0,就是偶数。
因为和1相&,除了第一位外,其他位都变成了0,而且二进制判断奇偶数的办法就是看第一位是零还是1;
性质运用
例题1
找到二进制中1的个数
1
2
3
4
5
6
7
8
9
10
| public static int countOne(int n){
int count = 0;
while(n != 0){
if(n & 1==1){
count++;
}
n = n >>> 1;
}
return count;
}
|
例题2
判断是否是二的整数次方
1
2
3
| public static boolean isPowerOfTwo(int n){
return (n>0) && ((n& (n-1))==0);
}
|
因为这里如果是二的整数次方的话,有最高位为1其他位为零的性质,那如果它减去1的话,就变成全是1的数了。刚好&,就变成0;
^ (异或)
异或的运算
对于两个二进制数 1010 和 1100,进行异或运算的结果是 0110。这是因为在进行异或运算时,每一位上==不同的数会产生一个1,而相同的数会产生一个0==。
异或的有趣性质
相同的数异或为零,零和任何数异或都为任何数本身。
==二进制由于除了1就是0,可以用异或来表示不进位的加法,但是其他进制的不进位加法就不是异或了==
性质运用
- 如果有一个数组中只有一个数字出现了偶数次,其他数字都出现了奇数次,那么对数组中的所有数字进行异或操作,最终的结果就是那个出现偶数次的数字。
例题1
- 有一个1-1000 的数组,只有唯一的元素值重复,其他均只是出现一次。每个数组元素只能被访问一次,请设计一个算法把它找出来,注意:不可以使用辅助空间。
如果可以使用辅助空间,没有什么限制条件的话,其实还有一种解法:就是用放到容器里,以值为下标,以出现的数量为容器的值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| public class 唯一成对的数 {
public static void main(String[] args) {
int N = 11;
int[] arr = new int[N];
for (int i = 0; i < arr.length; i++) {
arr[i] = i + 1;
}
arr[N - 1] = new Random().nextInt(N - 1) + 1;
int index = new Random().nextInt(N);
Util.swap(arr, index, arr.length - 1);
Util.print(arr);
solution(arr);
}
public static void solution(int[] arr) {
int res = 0;
System.out.println(arr.length);
for (int i = 1; i <= arr.length - 1; i++) {
res = (res ^ i);
}
for (int i = 0; i < arr.length; i++) {
res = arr[i] ^ res;
}
System.out.println(res);
}
}
|
例题2
1
2
3
4
| public static int abs(int num){
int mask = num >> 31;
return (num + mask) ^ mask;
}
|
注意:对于负数的>>31,其符号位为1,向右移动31位得到0x11111111,右移是补1的,结果就是-1.而且为啥负数要加-1呢?因为==补码表示法==的特点是:正数的补码和原码相同。
负数的补码是其对应正数的按位取反后加1。
例题3
1
2
3
4
5
| pubic static void swap(int a, int b){
int a = a ^ b;
int b = a ^ b;
int a = a ^ b;
}
|
这里用到了性质是交换律,异或连续和同一因子做异或运算,最终结果为自己。
A^B相当于==激发态==,如果再有原来的两数之一进行异或就会变回来那个两个数之一。
综合
交换奇偶位
指的是把奇数位和偶数位上的值作交换。这里也可以用多一个辅助空间解决。就是先转换成字符数组,然后循环交换n和n+1,每次n+2;但是这里使用位运算可以更加简单。
1
2
3
4
5
| public static int swapOddEvenBits(int i){
int odd = i & 0xAAAAAAAA;
int even = i & 0x55555555;
return add ^ even;
}
|
这里的是利用了&运算的保留作用:可以通过&1保留,&0去除,取出奇数位和偶数位。然后再通过异或的不进位加法的原理进行连接。
打印二进制的0~1之间的浮点实数表示
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public static void main(String[] args){
double num = 0.625;
StringBuilder sb = new StringBuilder("0.");
while(num>0){
double r = num *2;
if(r >= 1){
sb.append("1");
num = r -1;
}else{
sb.append("0");
num = r;
}
}
System.out.println(sb);
}
|
对于原始的二进制,比如15 ,是除以2,余数为1,商7,然后再把商进行一样的操作,把每个1和0组合在一起得到结果。
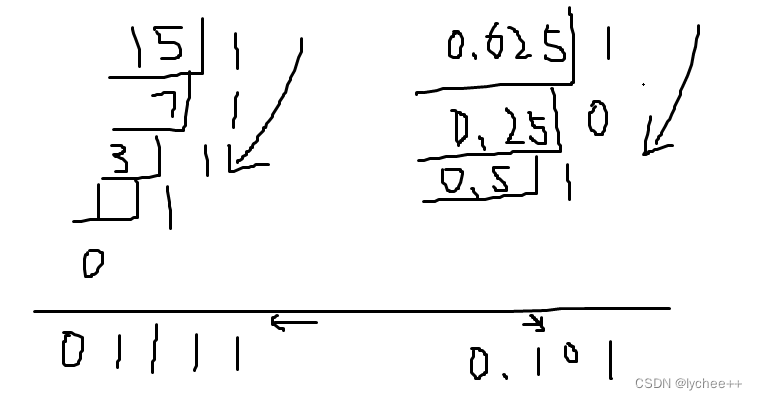
出现一次和出现k次
数组中只有一个数出现了1次,其他数字都出现了k次。请输出出现了1次的数。
==k个相同的k进制数作不进位的加法结果为0==
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| public class _11出现k次 {
public static void main(String[] args) {
int[] arr = {2, 2, 2, 9, 7, 7, 7, 3, 3, 3, 6, 6, 6, 0, 0, 0};
int len = arr.length;
char[][] res = new char[len][];
int k = 3;
int maxlength = 0;
for (int i = 0; i < len; i++) {
res[i] = new StringBuilder(Integer.toString(arr[i], k)).reverse().toString().toCharArray();
if (res[i].length > maxlength) {
maxlength = res[i].length;
}
}
int[] resArr = new int[maxlength];
for (int i = 0; i < len; i++) {
for (int j = 0; j < maxlength; j++) {
if (j >= res[i].length) {
resArr[j] += 0;
} else {
resArr[j] += (res[i][j] - '0');
}
}
}
int res1 = 0;
for (int i = 0; i < maxlength; i++) {
res1 += (resArr[i] % k) * Math.pow(k, i);
}
System.out.println(res1);
}
}
|
不规则进制才是真实的世界